Significant over-representation of pathway gene sets for a given gene list
Kidney Chromophobe (Primary solid tumor)
28 January 2016  |  analyses__2016_01_28
Maintainer Information
Citation Information
doi:10.7908/C1FQ9W0H
Maintained by Juok Cho (Broad Institute)
Cite as Broad Institute TCGA Genome Data Analysis Center (2016): Significant over-representation of pathway gene sets for a given gene list. Broad Institute of MIT and Harvard. doi:10.7908/C1FQ9W0H
Overview
Introduction

This pipeline inspects significant overlapping pathway gene sets for a given gene list using a hypergeometric test. For the gene set database, we uses GSEA MSigDB Class2: Canonical Pathways DB as a gene set data. Further details about the MsigDB gene sets, please visit The Broad Institute GSEA MsigDB

Summary

For a given gene list, a hypergeometric test was tried to find significant overlapping canonical pathways using 1320 gene sets. In terms of FDR adjusted p.values, top 5 significant overlapping gene sets are listed as below.

  • KEGG_GLIOMA, KEGG_PROSTATE_CANCER, KEGG_MELANOMA, KEGG_SMALL_CELL_LUNG_CANCER, KEGG_CELL_CYCLE

Results
For a given gene list, top significant overlapping canonical pathway gene sets

Table 1.  Get Full Table This table shows significant gene sets in which at least one gene is found and its FDR adjusted p.value is smaller than 0.3. the hypergeometric p-value is a probability of randomly drawing x or more successes(gene overlaps in gene set database) from the population (gene universe consisting of N number of genes) in k total draws(the number of input genes). The hypergeometric test is identical to the corresponding one-tailed version of Fisher's exact test. That is, P(X=x) = f(x| N,m,k). The FDR q.value was obtained for 1320 multiple comparison.

GS(gene set) pathway name gene.list GS size (m) n.NotInGS (n) Gene universe (N) n.drawn (k) n.found (x) p.value (p(X>=x)) FDR (q.value)
KEGG GLIOMA gene.list 65 45891 45956 11 3 4.420e-07 0.0003780
KEGG PROSTATE CANCER gene.list 89 45867 45956 11 3 1.146e-06 0.0003780
KEGG MELANOMA gene.list 71 45885 45956 11 3 5.779e-07 0.0003780
KEGG SMALL CELL LUNG CANCER gene.list 84 45872 45956 11 3 9.617e-07 0.0003780
KEGG CELL CYCLE gene.list 128 45828 45956 11 3 3.426e-06 0.0007924
BIOCARTA RB PATHWAY gene.list 13 45943 45956 11 2 4.057e-06 0.0007924
PID P53DOWNSTREAMPATHWAY gene.list 137 45819 45956 11 3 4.202e-06 0.0007924
BIOCARTA P53 PATHWAY gene.list 16 45940 45956 11 2 6.239e-06 0.0009332
BIOCARTA PML PATHWAY gene.list 17 45939 45956 11 2 7.070e-06 0.0009332
BIOCARTA ARF PATHWAY gene.list 17 45939 45956 11 2 7.070e-06 0.0009332
BIOCARTA TEL PATHWAY gene.list 18 45938 45956 11 2 7.952e-06 0.0009543
BIOCARTA TID PATHWAY gene.list 19 45937 45956 11 2 8.887e-06 0.0009776
BIOCARTA CTCF PATHWAY gene.list 23 45933 45956 11 2 1.314e-05 0.0013340
BIOCARTA EIF4 PATHWAY gene.list 24 45932 45956 11 2 1.433e-05 0.0013520
BIOCARTA G1 PATHWAY gene.list 28 45928 45956 11 2 1.962e-05 0.0017270
KEGG BLADDER CANCER gene.list 42 45914 45956 11 2 4.461e-05 0.0036800
KEGG PATHWAYS IN CANCER gene.list 328 45628 45956 11 3 5.697e-05 0.0044240
KEGG ENDOMETRIAL CANCER gene.list 52 45904 45956 11 2 6.862e-05 0.0050320
KEGG NON SMALL CELL LUNG CANCER gene.list 54 45902 45956 11 2 7.403e-05 0.0051430
KEGG P53 SIGNALING PATHWAY gene.list 69 45887 45956 11 2 1.211e-04 0.0071550

Figure 1.  Get High-res Image This figure is an event heatmap indicating gene matches across gene sets

Methods & Data
Input

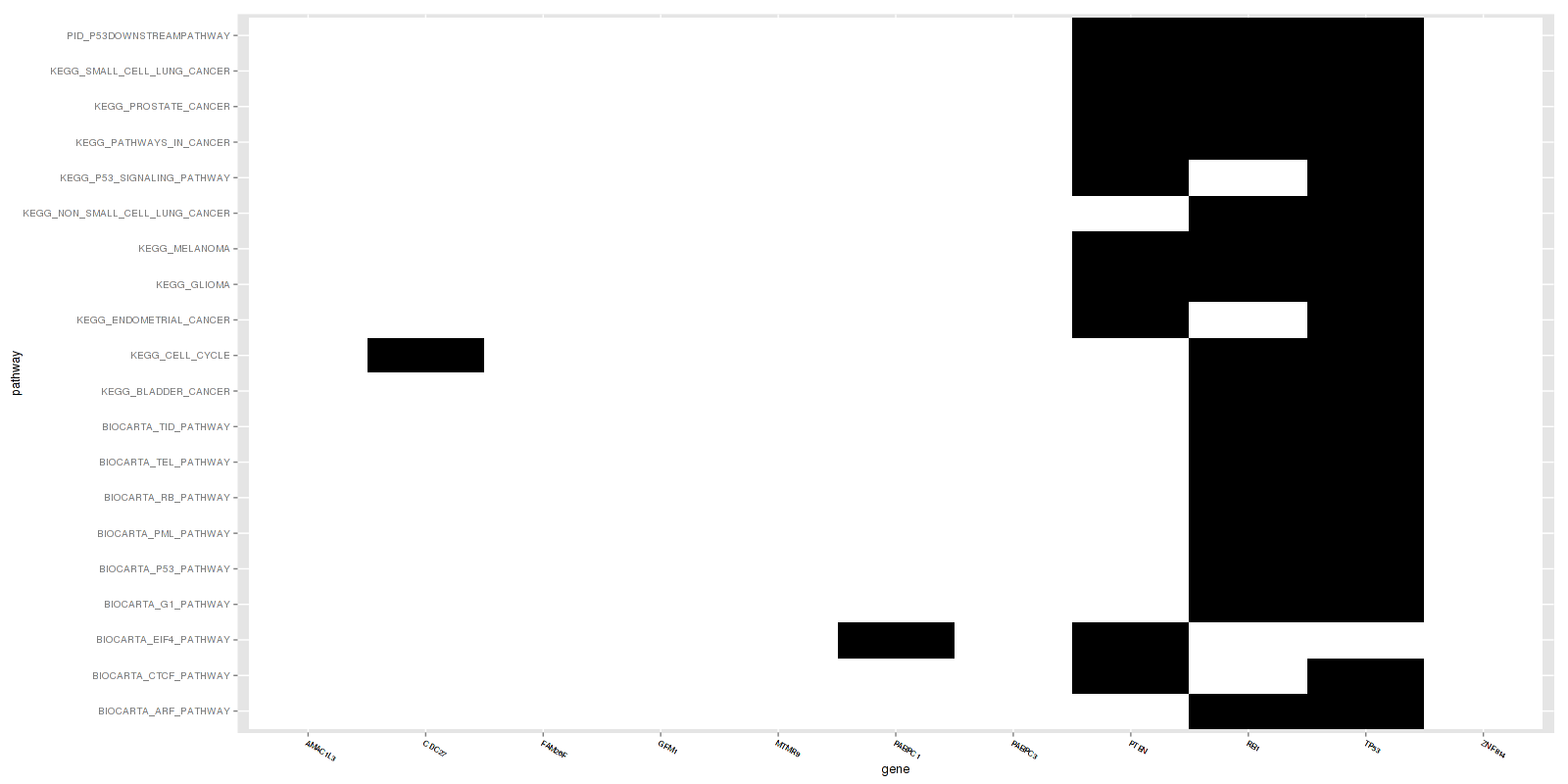
  • Gene set database = c2.cp.v4.0.symbols.gmt

Hypergeometric Test

For a given gene list, it uses a hypergeometric test to get a significance of each overlapping pathway gene set. The hypergeometric p-value is obtained by R library function phyper() and is defined as a probability of randomly drawing x or more successes(gene matches) from the population consisting N genes in k(the input genes) total draws.

  • a cumulative p-value using the R function phyper():

    • ex). a probability to see at least x genes in the group is defined as p(X>=x) = 1 - p(X<=x)= 1 - phyper(x-1, m, n, k, lower.tail=FALSE, log.p=FALSE) that is, f(x| N, m, k) = (m) C (k) * ((N-m) C (n-k)) / ((N) C (n))

  • The hypergeometric test is identical to the corresponding one-tailed version of Fisher's exact test.

    • ex). Fisher' exact test = matrix(c(n.Found, n.GS-n.Found, n.drawn-n.Found, n.NotGS- (n.drawn-n.Found)), nrow=2, dimnames = list(inputGenes = c("Found", "NotFound"),GeneUniverse = c("GS", "nonGS")) )

Download Results

In addition to the links below, the full results of the analysis summarized in this report can also be downloaded programmatically using firehose_get, or interactively from either the Broad GDAC website or TCGA Data Coordination Center Portal.

References
[1] Johnson, N.L., et al, Univariate Discrete Distributions, Second Edition, Wiley (1992)
[2] Berkopec, Aleš, HyperQuick algorithm for discrete hypergeometric distribution, Journal of Discrete Algorithms:341-347 (2007)
[3] Tamayo, et al, Molecular Signatures Database, MSigDB, PNAS:15545-15550 (2005)
Copyright © 2016 Broad Institute TCGA GDAC as part of the TCGA Research Network. All rights reserved.
Made with Nozzle